Sen. Bernie Sanders falsely claimed that “Mom is working, Dad is working, and the kids are working, and yet together they’re bringing in less disposable income today than a family did with one breadwinner 40 years ago.” In fact, Census data show an 85 percent increase in median disposable income for the households Sanders described from 1979 to 2014, in inflation-adjusted dollars.
Sanders made the claim at a rally on April 28 in Springfield, Oregon. He also made the claim two days earlier in West Virginia.
Sanders, April 26: But here is the fact — 40 years ago before the explosion of technology, before the cell phones and the space age technology and before the global economy, it was possible in America for one person — one breadwinner — to earn enough money to take care of the entire family.
One breadwinner could take — earn enough money to take care of the entire family. Well, then you got the whole global economy, all of the technology, you know what happens. Today, mom is out working, dad is out working, the kids are out working and they have less disposable income than a one breadwinner family had 40 years ago. Something is wrong with our economy.
Sanders urged the young people in the audience to “check it out, Google it, after you get out of here.” It takes more than a simple Google search, however, to find the statistics that pertain to Sanders’ claim. Once we were able to get those numbers, they show Sanders is wrong, by a long shot.
Families with at least three breadwinners (mom, dad and at least one child) — and Sanders describes families with at least two “kids” working — had much more disposable income in 2014 than a one-breadwinner family did 35 years earlier, as far back as the appropriate data go, adjusted for inflation.
The Sanders campaign told us that the Democratic presidential candidate was actually referring to discretionary income, not disposable. We’ll get to that, but first more on the claim Sanders actually made. Disposable income is total after-tax income, according to the Bureau of Economic Analysis.
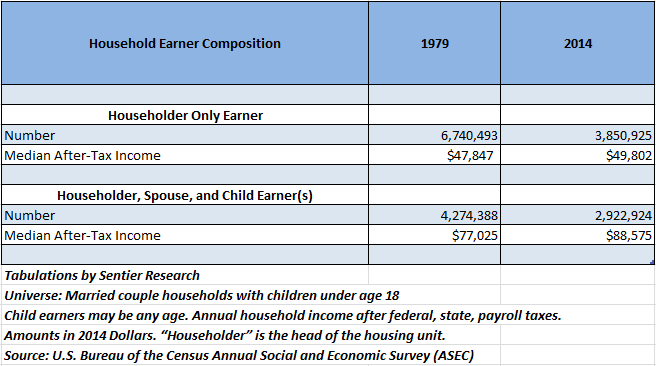
We contacted Sentier Research, which analyzes income and demographics data, and a spokesman said it would take some digging to get to the appropriate Census Bureau figures. Sentier then did the digging for us, using microdata from the Census’ Current Population Survey to find median (that’s the midpoint) disposable (after federal, state and payroll taxes) income for the families Sanders described.
As the chart below shows, median disposable income for a one-earner married couple household with at least one child under age 18 in 1979 was $47,847. In 2014, the median disposable income for a married couple household in which the husband, wife and at least one child works is $88,575. Those are both in 2014 dollars.
That’s a sizable increase in disposable income — an 85 percent jump, or $40,728 more. A married household with multiple breadwinners does much better today in terms of disposable income than a married household with one breadwinner did 35 years ago, the opposite of what Sanders claimed.
We also note that the number of one-earner married couple households with at least one child under 18 has decreased by about 2.9 million households in that time frame, but the number of married couple households in which the husband, wife and at least one child works has also gone down, by 1.4 million. So the situation Sanders describes with child earners is actually less common today than it was in the late 1970s.
Sanders’ Support
When we contacted the Sanders campaign about this claim, a spokesman sent us several statistics and other information on wages, income and spending. A few of those are related to, but don’t directly support, Sanders’ claim. We’ll go through some of those here. The campaign also said that Sanders was speaking “off the cuff” and meant to say discretionary income, not disposable.
Our fact-checking colleagues at PolitiFact.com looked into a similar claim Sanders had made about disposable income in the past — back in 2007, 2010 and 2011 — and also found he meant to say “discretionary.” So, Sanders has been making this claim about disposable income for years.
The Sanders campaign sent us Census figures on the mean, or average, household income for the third quintile (a good approximation for the “middle” of household income). That average had increased by 12 percent, or $5,759, from 1974 to 2014, a time period during which women’s labor force participation rate increased greatly, the campaign noted. (That’s expressed in 2014 numbers, and is similar to the median household income figures, which show an increase of $5,160, or 11 percent.)
But those figures are for all households, including those of single people, extended families, and single and multiple earners. There are more precise Census figures that pertain to Sanders’ claim, and they tell a much different story.
We can look specifically at family income — a family being two or more people related by birth, marriage or adoption — and the number of breadwinners per family (see Census Table F-12). The median income for a one-earner family in 1974 was $47,644 (again, in 2014 dollars). In 2014, a two-earner family’s median income was $91,362. That’s nearly a doubling for our one-breadwinner versus two-breadwinner family income over 40 years.
The median income for three-earner and four-earner families is even higher, and would more closely pertain to Sanders’ claim about the kids working, too: Three-earner median family income in 2014 was $110,110. Four-earner or more median family income was $132,565.
We can also look specifically at families in which only the husband worked full time and there was at least one child — median income of $68,541 in 1987, as far back as that dataset goes — and families in which both the husband and wife worked full time and there’s at least one child — median income of $115,144 in 2014. (Those figures are also in inflation-adjusted 2014 dollars; see Table F-16.)
These figures aren’t the after-tax, or disposable, income figures to which Sanders referred in his claim. The best figures for that are in the chart above.
Bottom line: Families or married couples with kids have substantially greater median incomes, both before and after taxes, if they have more than one earner in 2014 than such families with only one earner did decades ago.
But what about discretionary income, which the Sanders campaign says is what the senator meant to say? There isn’t a standard definition of what constitutes discretionary income, but it would be what money is left over after taxes and basic necessities, such as housing, are purchased.
The Sanders campaign, using the Bureau of Labor Statistics’ Consumer Expenditure Survey, ran some calculations on the average food, housing, clothing, transportation and health care expenditures for middle-income households, showing that the average leftover “discretionary” after-tax income declined from 1972-73 to 2014. But as the Sanders campaign later acknowledged, that doesn’t tell us anything about discretionary income or spending for one-earner versus multiple-earner families. The campaign said the BLS figures illustrated Sanders’ point that families were more likely to have both parents working but see less discretionary income. But the figures don’t show that, either.
The Sanders campaign sent us one other citation that comes closer to supporting his claim, if we consider discretionary, rather than disposable income. But the numbers are debatable.
A 2003 book by Sen. Elizabeth Warren, “The Two-Income Trap,” includes calculations showing a two-earner family with kids in 2000 had less discretionary income (by about $800 for the year) than a one-earner family with kids in 1973. Warren’s discretionary spending includes day care for the two-earner family but not the one-earner, and the tax calculations include nearly all taxes, such as sales and property taxes, based on a 2000 report from the Tax Foundation, which noted an increase in state and local tax burdens, as well as the federal payroll tax from 1975 to 1998.
There are multiple ways to conduct such calculations, not only because of questions on what exactly to use for discretionary spending, but what to use for the income figures, the starting point. For instance, Warren uses the median income for a full-time male worker for her one-earner family and then, for the two-earner family, adds together the median male full-time and median female full-time income. But median income tends to be higher when considering only married men and women, as opposed to all men and women, a group that would include younger workers often earning lower income.
“All the evidence suggests married people are a little older (there aren’t as many 16-year-olds or 24-year-olds) and better educated,” Gary Burtless, a senior fellow in economic studies with the Brookings Institution, told us.
Warren’s two-earner couple earned a combined $67,800 in 2000. But Census figures for a married couple with at least one kid and a husband and wife who both worked full time show a median income of $75,731 in 2000. (Use the F-16 “current dollars” table.)
Our single-earner married couple back in 1973 may have earned more than the median full-time male worker overall, too, but the Census’ detailed table doesn’t go back that far. We can only go back to 1987, when a family in which the husband worked full-time, the wife didn’t and there was at least one child under age 18 earned $68,541 in median income, in 2014 dollars. That’s higher than the median income for all full-time male workers in 1987: $51,743 in 2014 dollars.
That doesn’t mean Warren’s calculations were necessarily wrong, but there’s more than one way to calculate discretionary spending for various types of families. And Warren’s figures don’t even address Sanders’ claim, in which he said “the kids are out working” too.
Burtless told us in an email that Sanders’ claim is “a very tough claim to assess,” because we’d have to decide what qualified as discretionary spending and how much to subtract from families’ incomes.
“I can imagine that if you construct your couple carefully (and subtract just the right spending items to be consistent with your ‘discretionary income’ definition) you can get the result Sen. Sanders mentioned,” Burtless said. “Those calculations will depend on judgement calls, so it may be murky whether Sen. Sanders’ statement is clearly right or clearly wrong.”
Sanders is clearly wrong, however, on the disposable income of one-earner versus two- or multiple-earner families, the claim he made twice recently and several times in the past. Those multiple-earner families have a much higher median disposable income than one-earner families did in the 1970s.
https://www.sharethefacts.co/share/842f04f4-6418-43b3-b99c-7aac9c44a550